Tidyverse实例操作(4)

先将问题分解，然后用自带数据集或自编数据集设计一个简单实例，最后尝试写代码调试逐步解决问题，是非常有效的一种思维方式。
tidyverse
Author

Lee

Published

March 29, 2023

1 整洁数据的统计分析流程案例

1.1 生成数据并清洗

# 生成数据
set.seed(123)
df <- tibble(
  Sample = rep(c("A", "B", "C"), each = 7),
  root = c(rnorm(7, 10), rnorm(7, 5), rnorm(7, 21)),
  leaf = c(rnorm(7, 9), rnorm(7, 4), rnorm(7, 32)),
  stem = rnorm(21, 8)
)
df
# A tibble: 21 × 4
   Sample  root  leaf  stem
   <chr>  <dbl> <dbl> <dbl>
 1 A       9.44  8.78  6.73
 2 A       9.77  7.97 10.2 
 3 A      11.6   8.27  9.21
 4 A      10.1   8.37  6.88
 5 A      10.1   7.31  7.60
 6 A      11.7   9.84  7.53
 7 A      10.5   9.15  8.78
 8 B       3.73  2.86  7.92
 9 B       4.31  5.25  8.25
10 B       4.55  4.43  7.97
# ℹ 11 more rows
# 数据重塑
df1 <- df %>%
  pivot_longer(-Sample,
    names_to = "Tissue",
    values_to = "value"
  )
df1
# A tibble: 63 × 3
   Sample Tissue value
   <chr>  <chr>  <dbl>
 1 A      root    9.44
 2 A      leaf    8.78
 3 A      stem    6.73
 4 A      root    9.77
 5 A      leaf    7.97
 6 A      stem   10.2 
 7 A      root   11.6 
 8 A      leaf    8.27
 9 A      stem    9.21
10 A      root   10.1 
# ℹ 53 more rows

1.2 数据分析

# 分组正态性检验
df1 %>%
  group_by(Sample, Tissue) %>%
  shapiro_test(value)
# A tibble: 9 × 5
  Sample Tissue variable statistic      p
  <chr>  <chr>  <chr>        <dbl>  <dbl>
1 A      leaf   value        0.992 0.996 
2 A      root   value        0.890 0.277 
3 A      stem   value        0.923 0.491 
4 B      leaf   value        0.867 0.174 
5 B      root   value        0.980 0.959 
6 B      stem   value        0.765 0.0182
7 C      leaf   value        0.912 0.411 
8 C      root   value        0.982 0.970 
9 C      stem   value        0.892 0.283 
# 批量绘制Q-Q图-分面
ggplot(df1, aes(sample = value)) +
  stat_qq() +
  stat_qq_line(color = "red") +
  facet_wrap(Sample ~ Tissue, scales = "free")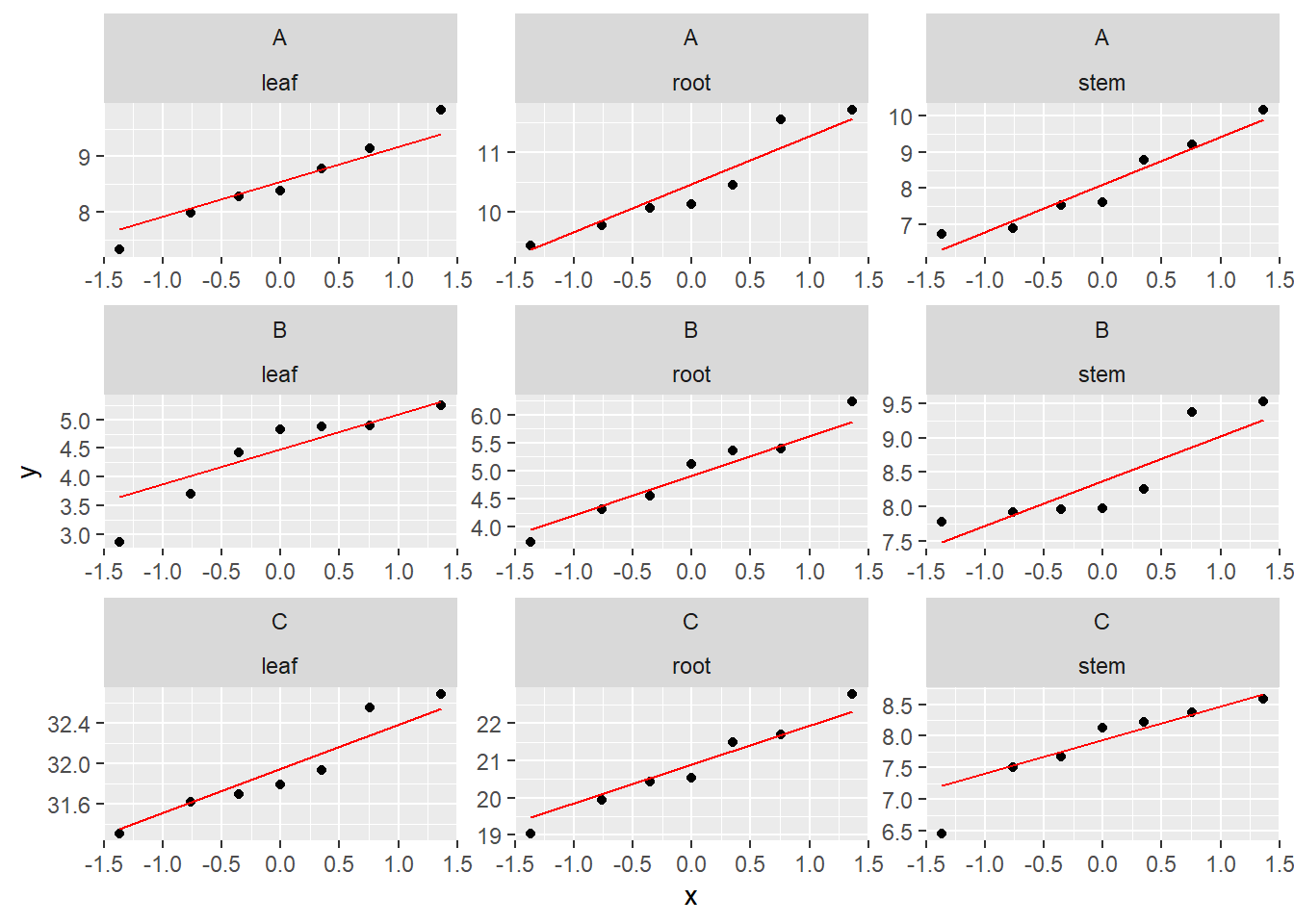

1.3 可视化

# 准备数据
df2 <- df1 %>%
  group_by(Tissue, Sample) %>%
  summarise(mu = mean(value), se = sd(value), .groups = "drop")
df2
# A tibble: 9 × 4
  Tissue Sample    mu    se
  <chr>  <chr>  <dbl> <dbl>
1 leaf   A       8.53 0.821
2 leaf   B       4.41 0.840
3 leaf   C      31.9  0.504
4 root   A      10.4  0.872
5 root   B       4.96 0.822
6 root   C      20.8  1.25 
7 stem   A       8.13 1.28 
8 stem   B       8.39 0.732
9 stem   C       7.85 0.724
# 可视化
df2 %>%
  ggplot(aes(Tissue, mu, fill = Sample)) +
  geom_col(position = "dodge") +
  geom_errorbar(aes(ymax = mu + se, ymin = mu - se),
    width = 0.5,
    position = position_dodge(0.9)
  ) +
  ylim(0, 40) +
  geom_segment(x = 0.7, y = 8 + 3, xend = 0.7, yend = 33 + 3) +
  geom_segment(x = 0.7, y = 33 + 3, xend = 1.3, yend = 33 + 3) +
  geom_segment(x = 1.3, y = 33 + 3, xend = 1.3, yend = 33) +
  annotate("text", x = 1, y = 33 + 4, label = "***") +
  theme_classic()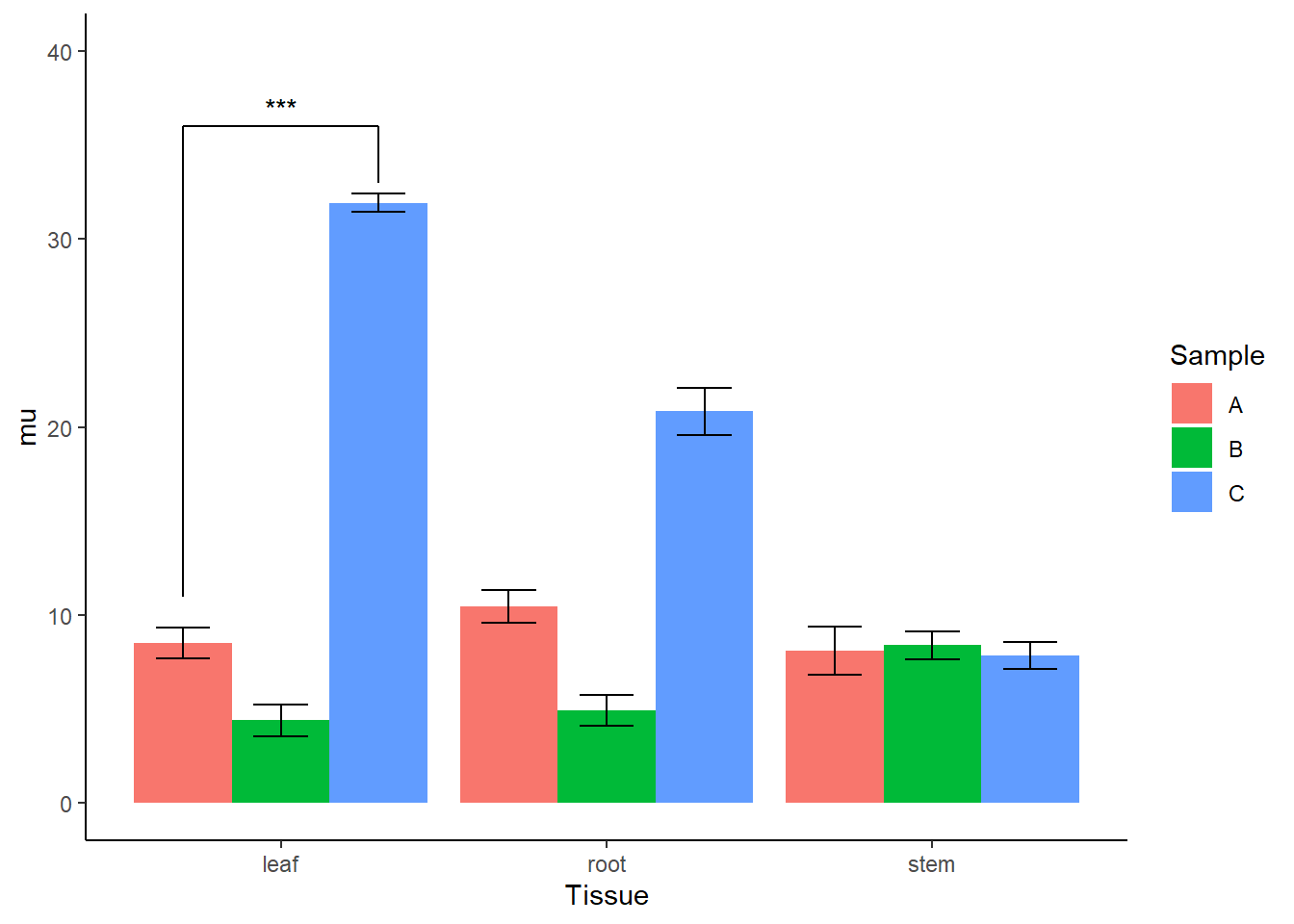

2 复杂重复随机抽样+批量建模

假设一个问卷有20题，100个被试作答，作答结果是0/1计分，每题答对得1分，答错得0分。

数据中，一行是一道题，想从这20题中随机抽19题，抽10次，计算这19题的某指标；然后随机抽18题，抽10次，计算这18题的某指标；然后随机抽17题，抽10次，计算这17题的某指标。。。一直到随机抽10题。

我们以mtcars数据集的前二十行为例，指标选择简单回归模型的\(R^2\).

library(tidyverse)
library(rsample)
df <- mtcars[1:20, ]
df
                     mpg cyl  disp  hp drat    wt  qsec vs am gear carb
Mazda RX4           21.0   6 160.0 110 3.90 2.620 16.46  0  1    4    4
Mazda RX4 Wag       21.0   6 160.0 110 3.90 2.875 17.02  0  1    4    4
Datsun 710          22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
Hornet 4 Drive      21.4   6 258.0 110 3.08 3.215 19.44  1  0    3    1
Hornet Sportabout   18.7   8 360.0 175 3.15 3.440 17.02  0  0    3    2
Valiant             18.1   6 225.0 105 2.76 3.460 20.22  1  0    3    1
Duster 360          14.3   8 360.0 245 3.21 3.570 15.84  0  0    3    4
Merc 240D           24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
Merc 230            22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
Merc 280            19.2   6 167.6 123 3.92 3.440 18.30  1  0    4    4
Merc 280C           17.8   6 167.6 123 3.92 3.440 18.90  1  0    4    4
Merc 450SE          16.4   8 275.8 180 3.07 4.070 17.40  0  0    3    3
Merc 450SL          17.3   8 275.8 180 3.07 3.730 17.60  0  0    3    3
Merc 450SLC         15.2   8 275.8 180 3.07 3.780 18.00  0  0    3    3
Cadillac Fleetwood  10.4   8 472.0 205 2.93 5.250 17.98  0  0    3    4
Lincoln Continental 10.4   8 460.0 215 3.00 5.424 17.82  0  0    3    4
Chrysler Imperial   14.7   8 440.0 230 3.23 5.345 17.42  0  0    3    4
Fiat 128            32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
Honda Civic         30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
Toyota Corolla      33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1

2.1 复杂随机重复抽样

使用rsmaple包中的mc_cv()函数(蒙特卡洛交叉验证抽样)，参数prop设定交叉比例，times设定重复次数。

在依次所要抽的题数（行数）：19, 18, ..., 10 上循环迭代，每次抽样的交叉比例就是：19/20, 18/20, ..., 10/20。

set.seed(1)

rsm <- map_dfr(19:10, ~mc_cv(df, prop = .x/20, times = 10))
rsm
# A tibble: 100 × 2
   splits         id        
   <list>         <chr>     
 1 <split [19/1]> Resample01
 2 <split [19/1]> Resample02
 3 <split [19/1]> Resample03
 4 <split [19/1]> Resample04
 5 <split [19/1]> Resample05
 6 <split [19/1]> Resample06
 7 <split [19/1]> Resample07
 8 <split [19/1]> Resample08
 9 <split [19/1]> Resample09
10 <split [19/1]> Resample10
# ℹ 90 more rows

从冲抽样对象split中将数据提取出来，使用analysis()函数。splits函数为列表列，需要使用map()函数。

rsm <- rsm %>% 
  mutate(data = map(splits, analysis))
rsm
# A tibble: 100 × 3
   splits         id         data          
   <list>         <chr>      <list>        
 1 <split [19/1]> Resample01 <df [19 × 11]>
 2 <split [19/1]> Resample02 <df [19 × 11]>
 3 <split [19/1]> Resample03 <df [19 × 11]>
 4 <split [19/1]> Resample04 <df [19 × 11]>
 5 <split [19/1]> Resample05 <df [19 × 11]>
 6 <split [19/1]> Resample06 <df [19 × 11]>
 7 <split [19/1]> Resample07 <df [19 × 11]>
 8 <split [19/1]> Resample08 <df [19 × 11]>
 9 <split [19/1]> Resample09 <df [19 × 11]>
10 <split [19/1]> Resample10 <df [19 × 11]>
# ℹ 90 more rows

2.2 批量建模

rsm %>% 
  mutate(model = map(data, ~ lm(mpg ~ disp, .x)),
         rsq = map_dbl(model, ~ summary(.x)$r.squared))
# A tibble: 100 × 5
   splits         id         data           model    rsq
   <list>         <chr>      <list>         <list> <dbl>
 1 <split [19/1]> Resample01 <df [19 × 11]> <lm>   0.736
 2 <split [19/1]> Resample02 <df [19 × 11]> <lm>   0.777
 3 <split [19/1]> Resample03 <df [19 × 11]> <lm>   0.764
 4 <split [19/1]> Resample04 <df [19 × 11]> <lm>   0.751
 5 <split [19/1]> Resample05 <df [19 × 11]> <lm>   0.751
 6 <split [19/1]> Resample06 <df [19 × 11]> <lm>   0.749
 7 <split [19/1]> Resample07 <df [19 × 11]> <lm>   0.749
 8 <split [19/1]> Resample08 <df [19 × 11]> <lm>   0.761
 9 <split [19/1]> Resample09 <df [19 × 11]> <lm>   0.764
10 <split [19/1]> Resample10 <df [19 × 11]> <lm>   0.777
# ℹ 90 more rows