大体上,统计学可分为描述性统计学和推断性统计学两大类。
- 描述性统计与推断统计结合:描述性统计用于检查数据的分布和特征,为假设检验、回归分析等提供基础。例如,在进行t检验前或ANOVA分析(方差分析)前,使用均值、标准差等检查数据合理性。
- 描述性统计与建模分析结合:变量间的相关性分析(相关矩阵)为多元线性回归或Cox回归提供自变量和筛选依据。例如,利用数据分布与偏态分析结果决定是否进行对数转换或非参数检验。
- 描述性统计与机器学习结合:描述性统计用于特征工程中的数据清洗、异常值检测和变量筛选。在随机森林或决策树模型中,分类变量与连续变量的描述性统计结果可以作为初始特征分析的依据。
1 描述性统计学
1.1 什么是描述性统计?
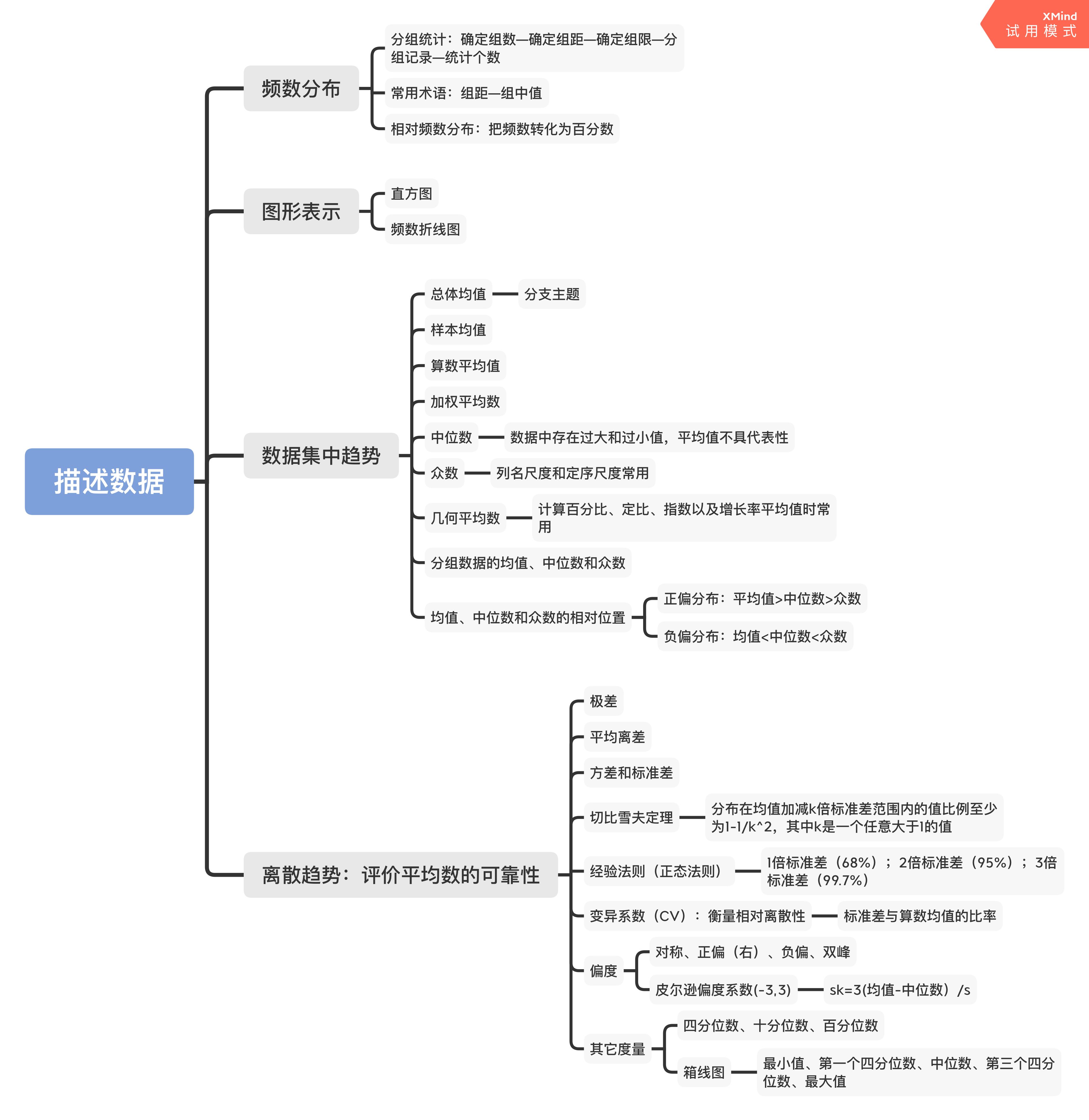
描述性统计学就是描述数据长什么样的统计学:最大值最小值、平均数、数据是集中还是离散,这都是在对数据进行描述。我们在做数据分析的时候,需要在数据中发现规律,但这一个前提就是我们要知道这组数据长什么样。就像男生想要追求一个女孩子时,需要充分了解这个女孩子,才能对症下药、投其所好一样。常见的描述数据的方法如下图所示:
1.2 描述性统计的应用内容
如图 图 1 所示为描述数据的主要方法。
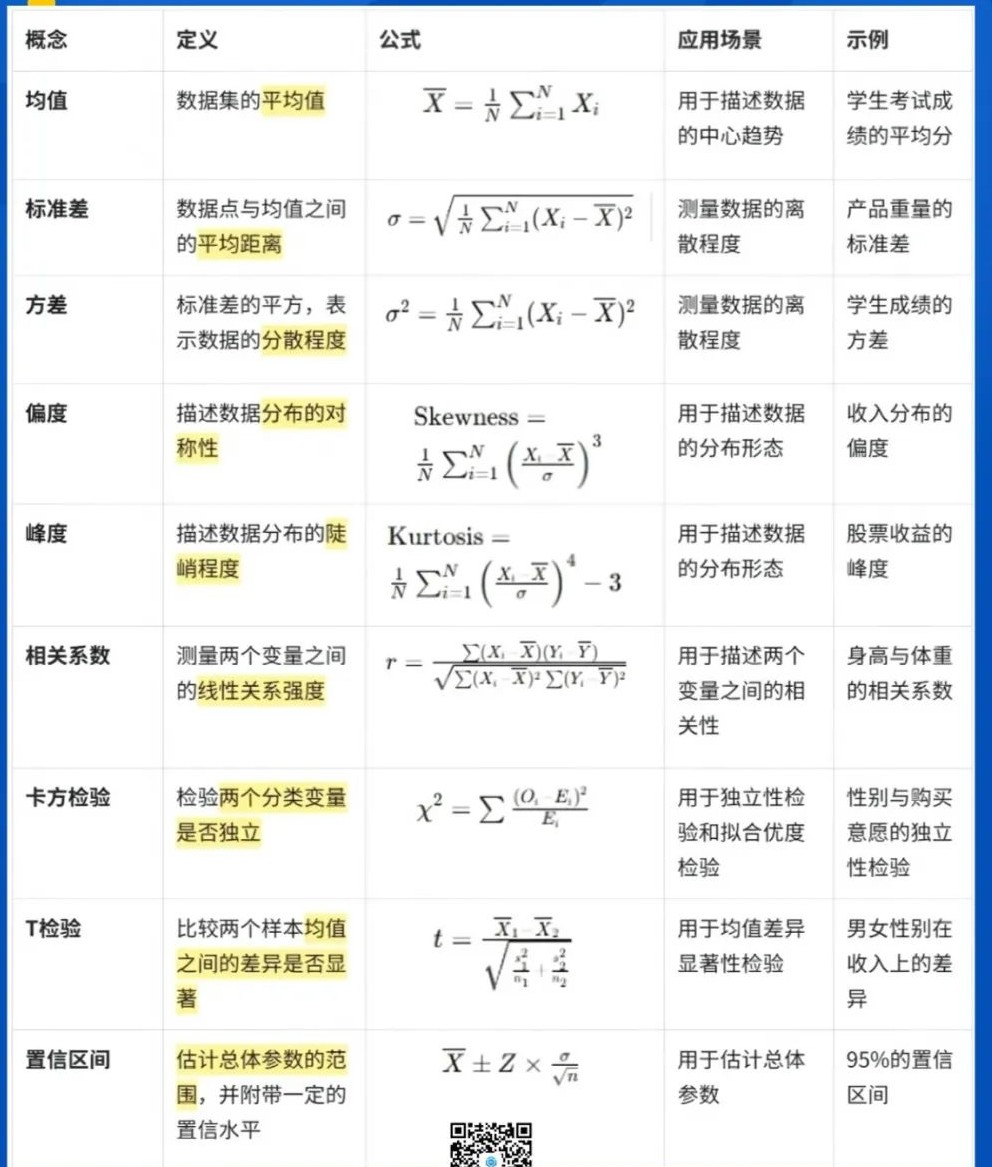
如图 图 2 所示为统计学的一些基础知识点。
1.3 抽样方法和中心极限定理
通常情况下的总体数量十分庞大,对其全体进行研究显然是不现实的,这是需要进行抽样。抽样,就是为了检测总体而从总体重抽出一个样本进行检测,以样本检测的结果来推断总体情况的一种方法。常见的抽样方法如下图所示。
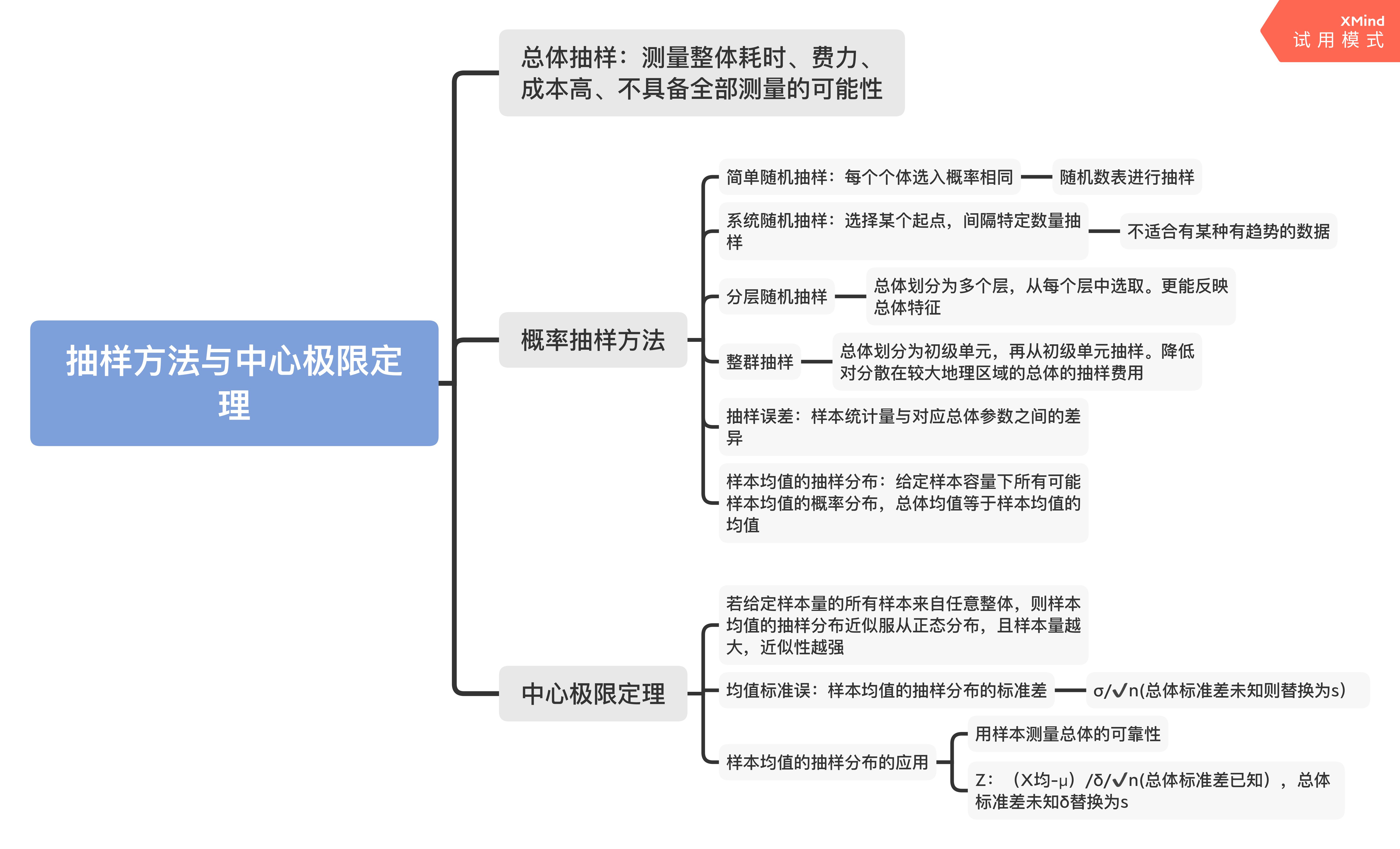
1.4 中心极限定理
根据中心极限定理:若给定样本量的所有样本来自任意整体,则样本均值的抽样分布近似服从正态分布,且样本量越大,近似性越强。
当样本量大于30的时候符合中心极限定理,样本服从正态分布;当样本量小于30的时候,总体近似正态分布时,此时样本服从t分布。样本的分布形态决定了我们在假设检验中采用什么方法去检验它。
2 统计推断
2.1 基本步骤
推断统计顾名思义就是从样本特征推断总体的特征。而这个推断的过程即所谓的假设检验。这个过程首先需要明确问题是什么?然后确定证据是什么?判断标准是什么?最后做出结论。即对应假设检验的几个步骤:
- 提出原假设
- 确定显著性水平(原假设为真时,拒绝原假设的概率)。
- 选择检验统计量。
- 建立决策准则。
- 得出统计结论。
P值的计算公式:
根据t值,查找t表格,得到P值。(或直接在R中进行计算)
2.2 假设检验的三种类型
在 R 语言中,有大量的函数可以对样本数据做检验,每一个函数对应一个或多个检验问题。其中:
- 单样本检验、两样本检验和多样本检验都只针对连续数据。
- 计数数据检验针对离散数据,不区分总体数量。
- 配对样本检验是两样本检验中的特殊情况,不分连续还是离散,不分两个样本还是多个样本,多个样本就是两两配对检验。
- 前面都是关于某个特征统计量的检验,对分布的检验涉及样本点是否来自正态分布,样本点是否独立和平稳,样本点是否来自某一分布,两个样本是否来自相同分布等。
- 单样本检验:检验单个样本的平均值是否等于目标值。
- 相关配对检验:检验相关或配对观测之差的平均值是否等于目标值。
- 独立双样本检验:检验两个独立样本的平均值之差是否等于目标值。
2.3 不同的统计检验方法
- Z检验:一般用语大样本(样本容量大于30)平均值差异性检验的方法。采用标准正态分布的理论来推断差异发生的概率,从而比较两个平均数间差异是否显著。
- t检验:用于样本含量较小(样本容量小于30),总体标准差未知的正态分布样本。
- F检验:又叫方差齐性检验,用于双样本t检验中,检验两个样本的方差是否有显著性差异,是选择t检验方式的前提条件。
- 卡方检验:主要用于检验两个或两个以上样本率或构成比之间差别的显著性,也可检验两类事物之间是否存在一定的关系。
- ANOVA:方差分析,用于比较三个或更多样本的均值差异,常用于多组数据的比较。单因素 ANOVA 用于单一因子对响应变量的影响分析。
t检验用来检测数据的准确度,检测系统误差;f检验用来检测数据的精密度,检测偶然误差。
是双尾检测还是单尾检测与我们提出的原假设有关。比如说我们检测中国和日本人民的学历是否有差异,如果原假设是中国人学历=日本人学历,原假设成立需要拒绝两个可能,一是中国人学历大于日本人学历,二是日本人学历大于中国人学历,此时我们就需要进行双尾检验。而原假设如果是中国人学历大于日本人学历,原假设成立只需要拒绝一个可能,即中国人学历小于日本人学历,此时就需要进行单尾检验。
2.4 置信区间与置信水平
置信区间[a, b]的计算公式如下,式中的z由置信水平决定。
2.5 效应量
通过假设检验得出的结论,只能了解样本是否有差异,无法得知这个差异到底有多大。这时就需要效应量出场了。
效应量指标是衡量差异大小(效果显著性)的指标,主要包括差异指标和相关性指标两大类。
2.5.1 差异指标(
| 效应量d值 | 差异大小(效果显著) |
|---|---|
| d=0.2 | 小 |
| d=0.5 | 中 |
| d=0.8 | 大 |
2.5.2 相关度指标(
| 效应量d值 | 差异大小(效果显著) |
|---|---|
| 小 | |
| 中 | |
| 大 |
3 数据统计分析报告一般格式内容
- 描述性统计分析
描述数据集基本情况。
假设检验:
- 设定假设检验的APA格式:
t (df) = ×.xx, p = .xx (α=.xx),检验方向
- 设定假设检验的APA格式:
置信区间/置信水平
效应量
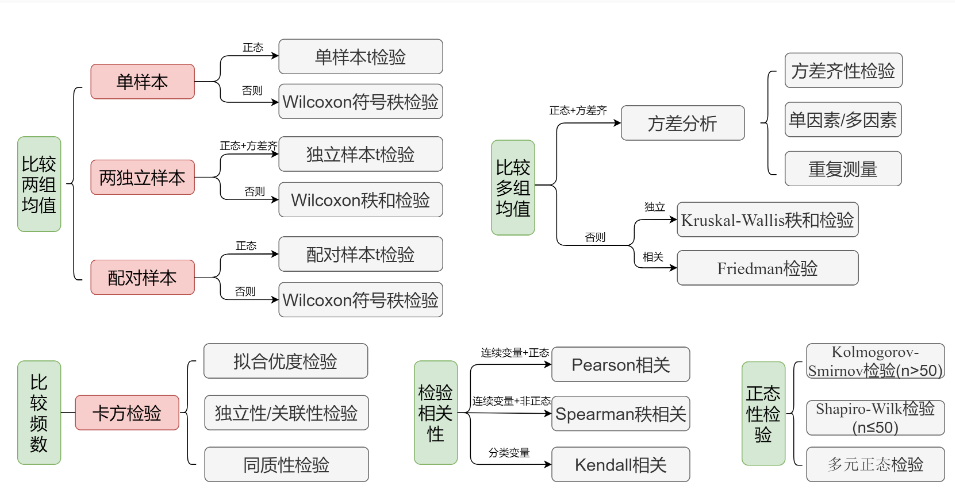
4 常用假设检验的适用情况
基于理论的假设检验,可分为两类:
参数检验:要求样本来自的总体分布已知,对总体参数进行估计;优点是对数据信息充分利用,统计分析效率高;缺点是对数据要求高、适用范围有限。
非参数检验:不依赖数据的总体分布,也不对总体参数进行推断;优点是不受总体分布限制,适用范围广,对数据要求不高;缺点是检验功效相对较低,不能充分利用数据信息。 选择原则:首先考察是否满足参数检验的条件,若满足首选参数检验,若不满 足只能采用非参数检验。